• 方法用意

public static int highestOneBit(int i) {        // HD, Figure 3-1        i |= (i >>  1);        i |= (i >>  2);        i |= (i >>  4);        i |= (i >>  8);        i |= (i >> 16);        return i - (i >>> 1);    }

　　如果i为负数，则统一返回-2³¹ = -2147483648

　　如果i=0，则统一返回0

　　如果i为正数，则返回i二进制表示的最高位为最高位，其余右边都补0的一个数。例如 i = 3 ，二进制是 0011，则返回的结果是 0010 = 2

• 算法过程解密

　　假设 i = 17，二进制表示为 00000000 00000000 00000000 00010001 

　　第一步，i |= (i >> 1) 计算过程

　　

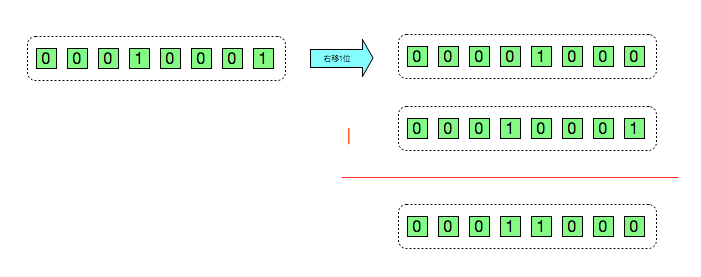
　　此时 i = 24 ，二进制表示为 00000000 00000000 00000000 00011000 

　　第二步，i |= (i >> 2) 计算过程

　　

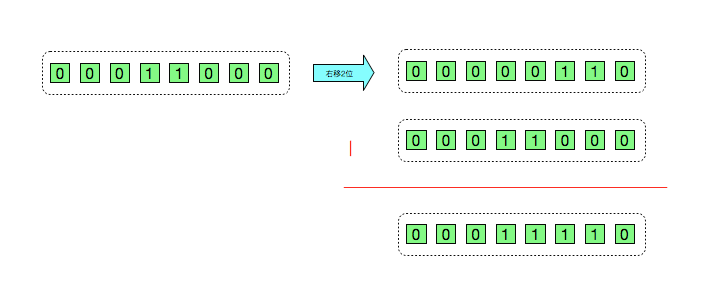
　　此时i = 30,二进制表示为 00000000 00000000 00000000 00011110 

　　第三步，i |= (i >> 4)计算过程

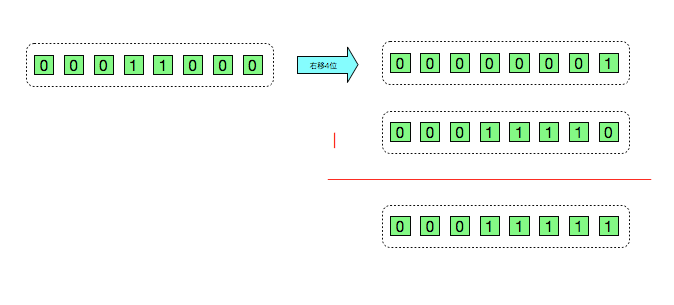
　　此时 i = 31，二进制表示为 00000000 00000000 00000000 00011111。这个时候就把原 i = 17 的最高位（第5位）开始都填充为1，这样第4步和第5步就都不会改变i的值了。

　　执行到（i - (i >>> 1)）之前 i一直为31。

　　最后一步，i - (i >>> 1)计算过程

　　

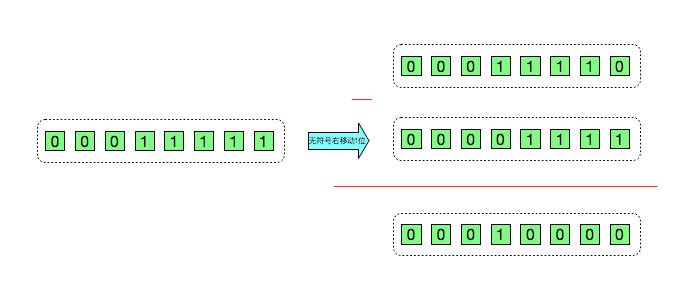
　　最后的结果是i = 16 

• 总结

1. 此方法的算法设计很精妙，性能非常高。
2. 整数的最大数是01111111 11111111 11111111 11111111，所以要经过上面1+2+4+8+16=31位的移动，才能确保取到从左边数31位的数字。
3. 负整数的首位，也即是符号位是1，经过i - (i >>> 1)计算，也就能得到最小的负整数10000000 00000000 00000000 00000000，所以负数执行此方法统一得到的值是-2147483648。